HÌNH ẢNH THỰC TẾ DỰ ÁN NLE THỰC HIỆN:




PUZZLE PARKING VEHICLE PARKING SYSTEM (CONSTRUCTION TYPE)
As the most used parking system, it is the Semiautomatic type (semi-automatic) in which the driver must back the car into the pallet and go out to the parking lot, then the system operator will manipulate to put the car into position. parked.
The system of putting the car in / out the parking lot by moving sideways and up and down of the pallet shape. The system is composed of separate blocks. Usually each Block will have a maximum of 6 rows x 6 floors. Maximum number of vehicles is 32/01 Block. At the same time the vehicle can enter / exit the parking lot in these blocks without having to wait for the operation of the adjacent Block.
The maximum time to take a car is 60 seconds with the system using 2 to 3 floors and 90 seconds with the system using 4 to 5 floors.
Regarding the layout installed on the ground, there is a type of completely floating on the ground, there is 01 type of float, partly underground
 Fully floating type
Fully floating type
 Type a part to float partially underground
Type a part to float partially underground With the completely floating type on the ground, the disadvantage is that there must always be vacant positions in the rows for the operating system to bring the car in / out to the parked position. The maximum number of vehicles for each type will depend on the number of cargoes and the number of floors.
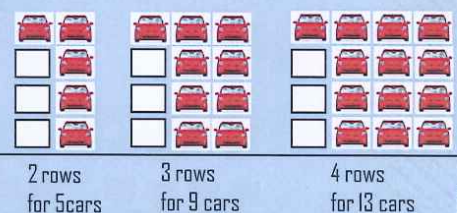
· If the number of car parks is: A
· Number of floors for parking: B
· Maximum number of vehicles allowed is: C = A + (B-1) x (A-1)
For example: The applicable system is of type: 2 rows x 4 floors for parking, the maximum number of vehicles to be arranged
C = 2+(2-1)x(4-1)= 2+1x3 = 5 cars
The system applied is type: 3 rows x 4 floors for parking, the amount is vacant:
C = 3+ (3-1)x(4-1) = 3+2x3 = 9 cars
Applicable system is type: 4 rows x 4 floors for parking, the number of vacant:
C = 4+ (4-1)x(4-1) = 4+3x3 = 13 xe
Maximum of the system is arranged 6 rows x 6 floors for parking. The maximum number of cars that can be stored per Block is: 6 + 5x5 = 31 vehicles.
Ø With the installation of a floating part and an underground part (the underground part is calculated from the cost of the car in / out to below), it is possible to take advantage of 100% parking position. For example, if there are 6 rows of cars with the same 6 floors, the maximum number of cars to be: 6x6 = 36 cars.
How the system works to put a car in a parked position is as follows:

| Step 1 |
Step 2 |
Step 3 |
Step 4 |
Step 5 |
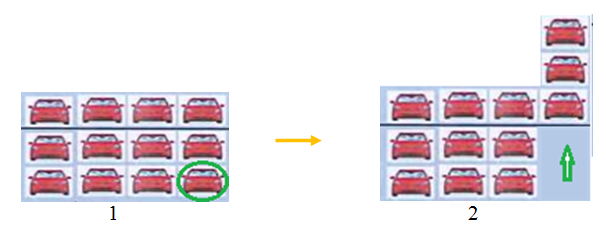
In the figure, we need to put the yellow car circled in step 5 into the parked position.
Step 1: Receive a parking order, the red circle pallet will be lowered to pick up the yellow car in step 5.
Step 2: The first white car in the first row of the first floor will be taken to the third floor in the direction of the blue arrow.
Step 3: All two rows of cars on the first and second floors simultaneously move by the green arrow to the left.
Step 4: The circled red pallet received the order will move straight to the first floor to catch the car to the parking spot.
Step 5: The driver will then drive the car back to the Pallet, turn off the engine and leave the car to get its car code.
How the system works to get a car out of the parked position is as follows:

| Step 1 |
Step 2 |
Step 3 |
Step 4 |
Step 5 |
In the picture, we need to take the orange-yellow car out to the parking lot.
Step 1: Receive a ride order, the red circle pallet will be lowered to return the car at the position like step 5.
Step 2: The first yellow car in the 3rd row of the 1st floor will be taken to the 3rd floor in the direction of the blue arrow.
Step 3: All 3 rows of cars will move to fill the vacant position in the direction of the green arrow to the right of the parking lot to make room for the Pallet carrying the orange car to move down.
Step 4: Pallet carrying orange car to be removed will move straight to the 1st floor to return the car in the direction of the green arrow.
Step 5: The driver will then be in the coachman and head out of the parking lot.
Ø With partially floating part, the maximum number of vehicles is 100% Pallet
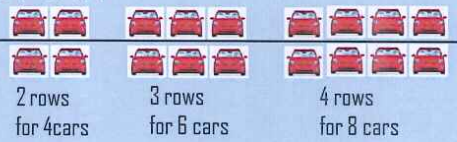
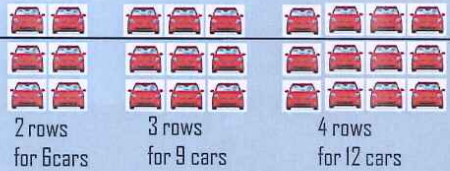
· Number of parking spaces is: A
· Number of parking floors is: B
· Maximum number of vehicles to purchase is: C = AxB
For example: The applicable system is of type: 2 rows x 4 floors for parking, the maximum number of vehicles to be arranged
C = 2x4 = 8 cars
The system applied is type: 3 rows x 4 floors for parking, the amount is vacant:
C = 3x4 = 12 cars
Applicable system is type: 4 rows x 4 floors for parking, the number of vacant:
C = 4x4 = 16 cars
Type 1 underground floor
Type 2 underground floors
In addition to the advantage of making the most of 100% of the Pallet garage, the downside is that the cost of building the system will be more expensive for the basement category and the lift system.
The way to get the car out of the parking lot is very simple. When receiving a call, the system will automatically lift the car's vertical column by the height of the vehicle in and out of the parking lot. Drive into the car and drive off the Pallet.
For example, if you want to take a car in the green area, the system will raise the column of 03 cars up to the position of car No. 2 with the car entrance and exit.